Hi!
I'm currently working on configuring a custom drone and need to configure the cameras and body to be in the right location with respect to the imu's. The configure extrinsics doc found here is a little confusing. I have two questions.
First, Translations:
"The Translation vector should represent the center of the child coordinate frame with respect to the parent coordinate frame in units of meters."
This line is a little confusing. Should the translation be in terms of the child or the parents coordinate frame?
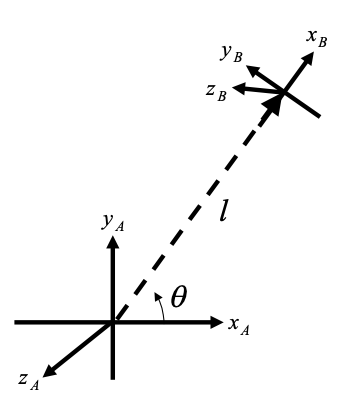
(parent:A child:B)
Following a normal homogenous transformation matrix, the translation is in terms of the child's coordinate frame (as above where l is the x translation in terms of the child), is this correct? (my inclination is no in this case)
Also is it the translation from the center of the parent to the child or the other way around (l vs negative l)?
Second imu1 and imu0 Confusion and Subsequent Transformations:
The imu1 and imu0 default extrinsics are noted as not correct but I am still confused
"RPY_parent_to_child": [0, 0, 0]
from
"extrinsics": [{
"parent": "imu1",
"child": "imu0",
"T_child_wrt_parent": [-0.0484, 0.037, 0.002],
"RPY_parent_to_child": [0, 0, 0]
}
Even though it is clear from the diagram that imu1 and imu0 do not share a common frame
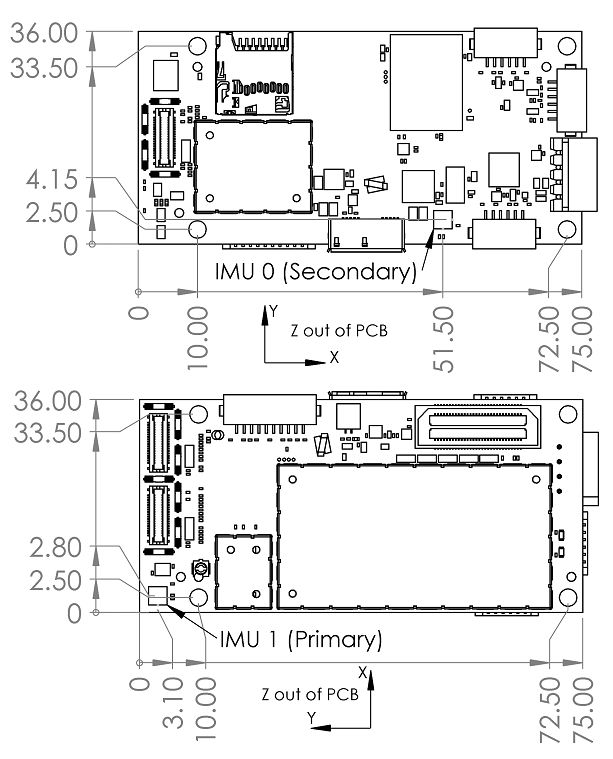
The docs seems to address this by saying:
"NOTE that voxl-imu-server rotates the IMU data into a common and more useful orientation such that both IMU’s appear to be oriented in FRD frame for the VOXL M500, flight deck, and Starling reference platforms. In the top image of the diagram above, this corresponds to X pointing Left, Y pointing to the right, and Z pointing out of the diagram. This conveniently allows the rotation matrix between IMU and body frame to be identity for most use cases."
So my question is, why is the imu1-imu0 transformation setting even there if it is a constant, and to which imu should I orient all of my cameras? Which frame is that?
Any help would be much appreciated transformation matrices can get quite tricky at times! 
Best,
Jamie